Sliding Block

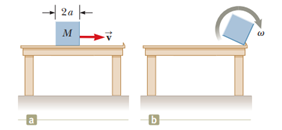
Problem Statement

A solid cube of side $2a$ and mass $M$ is sliding on a frictionless surface with a uniform velocity $v$, as shown. It hits a small obstacle at the end of the table, causing the cube to tilt, as shown. Find the minimum value of the magnitude of $v$ such that the cube tips over and falls off the table.

Note: The cube undergoes an inelastic collision at the edge.

Key Concepts

• Frictionless Motion: The cube slides without friction, conserving momentum and energy until the collision ^[1].
• Inelastic Collision: The collision at the edge is inelastic, meaning kinetic energy is not conserved, but momentum is ^[2].
• Tipping Condition: The cube will tip over if the rotational kinetic energy gained from the collision is sufficient to lift its center of mass over the edge ^[3].

Approach

1. Conservation of Angular Momentum: Use the conservation of angular momentum about the edge of the table to relate the initial velocity $v$ to the angular velocity $\omega$ after the collision ^[4].
2. Rotational Kinetic Energy: Calculate the rotational kinetic energy required to lift the cube's center of mass over the edge ^[5].
3. Minimum Velocity: Set the rotational kinetic energy equal to the potential energy change and solve for $v$ ^[6].

Solution

1. Angular Momentum Conservation:

   $$L_{\text{initial}}=Mva$$$$L_{\text{final}}=I\omega =\frac{5}{3}M{a}^2\omega$$$$Mva=\frac{5}{3}M{a}^2\omega ⟹\omega =\frac{3v}{5a}$$

2. Rotational Kinetic Energy:

   $$K{E}_{\text{rot}}=\frac{1}{2}I{\omega }^2=\frac{1}{2}\cdot \frac{5}{3}M{a}^2\cdot {\left(\frac{3v}{5a}\right)}^2=\frac{3}{10}M{v}^2$$

3. Potential Energy Change:

   $$\mathrm{\Delta }PE=Mga$$

4. Tipping Condition:

   $$K{E}_{\text{rot}}\ge \mathrm{\Delta }PE⟹\frac{3}{10}M{v}^2\ge Mga$$$$v^2\ge \frac{10}{3}ga⟹v\ge \sqrt{\frac{10}{3}ga}\approx 1.826\sqrt{ga}$$

Final Answer

The minimum value of $v$ required for the cube to tip over and fall off the table is:

Footnotes